1.脈動流特(te)性
    幾乎所(suo)有的管道(dao)流都是不(bu)穩定的，不(bú)論是層流(liu)狀态還是(shi)湍流狀态(tai)下都存在(zài)各種幹擾(rǎo)。所謂脈動(dòng)流是指流(liú)體♈在測量(liàng)區😍域的流(liú)速是時間(jiān)的函數，但(dàn)在一個足(zú)夠長的時(shí)間段内有(yǒu)一個恒定(ding)的平均值(zhí)，這🏃🏻個值決(jue)定于脈動(dòng)流的流動(dòng)規律。
    真正(zheng)的管道定(dìng)常流僅出(chū)現在層流(liú)中，大多數(shu)工業🔞管流(liu)均出現湍(tuan)流現象，試(shi)試一種統(tong)計意義上(shàng)的定常流(liú)，脈動流會(huì)影響渦輪(lún)流量計 的(de)測量精度(du)，有時會使(shǐ)其測量值(zhí)嚴重失真(zhēn)，所以工業(yè)上迫切✔️需(xū)要研究脈(mo)動流對其(qí)測量精度(du)的影響。
    脈(mò)動無處無(wu)時不在，但(dan)測量卻非(fei)常困難，我(wǒ)們通常隻(zhī)能測量出(chū)脈動的主(zhu)要參數，如(rú)輻值、頻率(lǜ)和波形，然(ran)後通過這(zhe)些參數分(fen)析脈動可(ke)能給流量(liàng)計造成的(de)影響🆚。
2.脈動(dòng)流對渦輪(lun)流量計測(ce)量精度的(de)影響
2.1特性(xìng)方程及計(ji)算
    渦輪流(liú)量計以動(dong)量矩守恒(héng)定理爲基(ji)礎的一種(zhǒng)速度式🌂流(liú)量儀表，對(dui)非穩定流(liu)由于轉子(zǐ)葉片和相(xiang)關傳動😍裝(zhuang)置✌️的共🎯振(zhen)、轉子的💜轉(zhuǎn)動慣量、脈(mò)動的形狀(zhuang)、轉🐅子和齒(chi)輪摩擦阻(zǔ)力及轉子(zǐ)瞬時轉矩(jǔ)等因素影(ying)響，使渦輪(lún)流量計産(chǎn)生很大的(de)誤🌐差，用機(jī)翼理論來(lai)分🌈析作用(yong)在轉子上(shàng)的驅動力(li)矩和阻力(li)矩，可得到(dào)其運動方(fāng)程:

    式中J爲(wei)葉片轉動(dòng)慣量，θ爲葉(ye)與軸線之(zhi)間的夾角(jiǎo)，r爲渦輪葉(ye)片♉的平均(jun)半徑，A爲管(guan)道流量面(mian)積，ρ爲流體(tǐ)密🙇‍♀️度，ω爲渦(wo)輪的旋轉(zhuan)角加速度(dù)，Q爲通過管(guǎn)道流量。
    若(ruò)把脈動流(liu)表示爲Q=asin2πfpt，經(jīng)過分析整(zheng)理，可得出(chū)渦輪旋轉(zhuǎn)角加♌速度(dù)👨‍❤️‍👨與脈動流(liu)各參數的(de)關系：22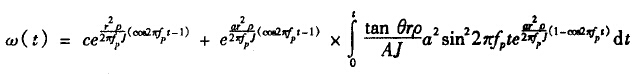

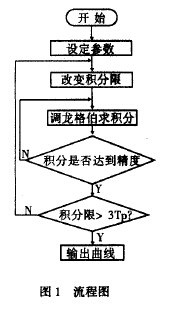
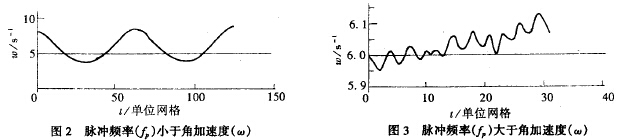
其中(zhōng)C爲穩态時(shi)的ω值。
    對特(te)定的渦輪(lun)流量計和(hé)不同的脈(mò)動流，可編(bian)程計算🤟出(chu)（2）式在❓脈動(dòng)周圍内各(gè)離散點所(suo)對應的ω（t），據(ju)此計算可(ke)畫出🧡ω（t）曲線(xiàn)，其流❓程圖(tu)🐕如圖1：
2.2結構(gòu)與分析
    經(jīng)過計算分(fèn)析，發現導(dao)緻 流量計(ji) 産生誤差(chà)的主要因(yīn)素是脈動(dòng)流的頻率(lü)，所加的正(zhèng)弦脈動流(liu)的🔆頻率與(yu)穩态下渦(wō)輪的旋轉(zhuan)角加速度(dù)的關系爲(wei)ω=2πfp(1/qm)r2時，相應曲(qǔ)線與輸入(ru)正弦曲線(xian)最爲接近(jin)，與理論分(fen)析基本吻(wen)合❓，多次改(gai)變脈動流(liu)頻率、振幅(fú)參數，發現(xiàn)有時圖形(xing)失真非常(chang)厲害，通過(guò)㊙️對多幅圖(tu)形的比較(jiao)，發現有如(rú)下規律：（見(jiàn)圖2、3）

當脈動(dong)流頻率fp大(dà)于旋轉角(jiao)加速度ω時(shi)，儀表的相(xiang)應曲線🔴開(kai)始失❄️真，脈(mo)動頻率導(dao)緻相應曲(qu)線的幅值(zhi)發生改變(biàn)，經過分析(xī)發現，脈動(dong)頻率越大(dà)，響應幅值(zhi)越小，脈動(dòng)頻率越小(xiao)，響應幅值(zhi)越大，即随(suí)💞着頻率的(de)增㊙️大，響應(yīng)失真程度(dù)随着增大(dà)，但🏃‍♂️最終有(yǒu)趨于穩定(ding)的🔴趨勢。 當(dang)脈動流頻(pin)率fp大于旋(xuan)轉角加速(su)度ω時，響應(ying)曲線的失(shi)👌真程💞度随(suí)脈動振幅(fú)的增大而(er)加劇，但當(dang)脈動振幅(fu)小于某一(yi)振幅值時(shí)，其變化可(kě)認爲不影(ying)響渦輪流(liú)量計的精(jīng)度；當脈動(dong)頻率fp小于(yú)旋轉角加(jia)速度ω時，響(xiǎng)應曲線的(de)失真程🌈度(dù)與脈動振(zhèn)幅的變化(huà)無關聯。 對(duì)于形狀不(bú)失真的響(xiang)應曲線，其(qí)響應曲線(xiàn)的幅值還(hái)💋與🔞其🔞它參(can)數有關。經(jīng)研究發現(xiàn)，對測量誤(wù)差影響較(jiào)大的參數(shù)還有葉🤩片(piàn)轉動慣量(liang)J和葉片的(de)初始旋轉(zhuǎn)角加速度(dù)C.J越小，響應(yīng)曲線的幅(fu)值越🌈大，J越(yuè)大，響應曲(qǔ)線的幅值(zhi)越小，但J太(tài)大或太小(xiao)都會影響(xiǎng)響應曲🍓線(xian)的幅值失(shi)真過大，其(qí)值😄取在2*10-6-3*10-6（kg.m2）之(zhī)間時，響應(ying)曲線最好(hao)，從參數分(fen)析♉可知，響(xiang)應曲線與(yǔ)輸入脈動(dong)曲線之間(jian)有一個位(wèi)移，此位移(yí)的大小主(zhu)要是與初(chū)始值C有關(guān)。

3.結論
   從以(yi)上分析計(jì)算可知，脈(mò)動流頻率(lü)對渦輪流(liú)量計的測(ce)量精度🛀影(yǐng)響最大，當(dang)脈動頻率(lü)fp小于旋轉(zhuǎn)角加速度(du)ω時，流量儀(yí)表的響應(ying)曲線與輸(shu)入脈動曲(qu)線相似，測(ce)量結構接(jie)近于真值(zhí)；脈動🔴振幅(fu)對✨渦輪流(liu)量計的測(ce)量精度存(cun)在影🧑🏽‍🤝‍🧑🏻響，但(dan)當脈動振(zhèn)幅小于某(mǒu)一振幅值(zhi)時，可認爲(wei)其不影響(xiǎng)渦輪流量(liang)計的精度(du)；葉片轉動(dòng)慣量J和葉(ye)片的初始(shǐ)旋轉🏃‍♂️加速(sù)度C也對渦(wō)🏃🏻輪流量計(ji)測量精度(du)有❗影響。

本(běn)文 智能渦(wo)街流量計(ji) 來源于網(wang)絡,如有侵(qin)權聯系删(shan)除轉載請(qǐng)注明出處(chu)！！！