摘要:小流量測(cè)量時,差壓式流量(liang)計
輸出的差壓與(yu)流量之間是非線(xian)性關系,在分散控(kong)制系統(DCS)中直接實(shi)施該非線性關系(xi)較困難。根據已知(zhī)标準孔🐆闆的💛徑比(bǐ)👣,用NURBS非均勻有理函(hán)數,拟合在特定應(ying)用📧條件下的标準(zhun)孔闆流量系數🌂公(gong)式;并用簡單的乘(chéng)法和加法運算,在(zài)DCS中用NURBS函數表示該(gai)非線性關系的輸(shu)入📱和輸出關系;最(zuì)後用非線性叠代(dai)算法确定在小流(liu)量🐆條件下的差壓(yā)和流量關系,從🔞而(er)實現小流量測量(liang)的在線非❌線性補(bǔ)償,提高了流量測(ce)♈量的精度。
差壓式(shi)流量計是常用的(de)流量測量儀表。
标(biāo)準孔闆
的流量系(xi)數經Reader-Harris/Gallagher修改,于1998年被(bei)采納作爲标準孔(kǒng)闆流出系數的計(jì)算公式。它對小流(liu)量時差壓式流量(liang)計的補償提供了(le)理論基礎,但在分(fèn)散控制系統(DCS)中實(shí)現有困難,爲此,提(ti)出兩種實施方法(fǎ):直🍉接用Reader-Harris/Gallagher公式,但在(zai)DCS上Reader-Harris/Gallagher公式實施困難(nan);針對特定标準孔(kong)闆,用NURBS函數拟🥰合标(biāo)準孔闆流出系數(shu)的Reader-Harris/Gallagher計算公式,并在(zài)DCS中實現。該方法既(ji)解決了💋小流量在(zài)線補償的實施問(wen)題🔴,也提高了差壓(yā)式流量計的測量(liàng)範圍度✂️和精度。
1NURBS樣(yang)條函數
1.1B樣條基函(hán)數
B樣條基樣條(basicspline)。1946年(nián)由舍恩貝格(Schoenberg)提出(chū),并在1972年由德布爾(ěr)和考克斯(deboor-Cox)分别獨(du)立給出B樣條計算(suàn)的标準算法[1-2]。理論(lun)上常采用截尾幂(mi)函數的差商定義(yì)B樣條曲線,實際應(ying)用則常采用B樣條(tiáo)的遞推定義。
B樣條(tiáo)曲線采用控制頂(dǐng)點定義曲線[1-2]。曲線(xian)方程可描述爲
![]()
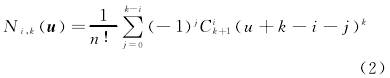
式(shi)中:Pi———控制多邊形的(de)頂點,i=0,1,…,n;Ni,k(u)———k次(k-1次)B樣條基(ji)函數,i=0,1,…,n。
其中,每個k次(ci)規範B樣條基函數(shu)稱爲規範B樣條,或(huò)簡稱B樣條。由于它(tā)由非遞減節點矢(shi)量u的序列T:u0≤u1≤…≤un+k所決定(ding)的k次分段多項式(shì),因而,稱爲k-1次多項(xiang)式樣條。
根據德布(bu)爾-考克斯的遞推(tui)公式,曲線方程可(ke)寫爲
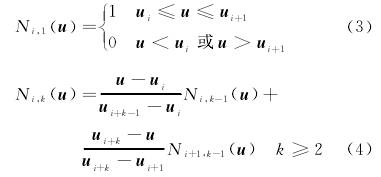
式中:i,k———下标,i表(biao)示序号,k表示次數(shù)。
1.2三次非均勻有理(li)B樣條函數
三次非(fēi)均勻有理B樣條函(hán)數描述爲
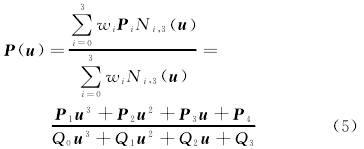
式中:wi———權(quan)因子,分别與控制(zhì)頂點Pi相聯系,(i=0,1,…,n);Ni,k(u)———節點(diǎn)矢量,u=[u0,u1,…,un+k+1]按遞推公式(shi)确定的k次規範B樣(yang)條基函數;P1,P2,P3,P4———分子系(xi)數,爲矢量;Q0,Q1,Q2,Q3———分母系(xì)數。B樣條基函數的(de)遞推公式見式(3)~式(shì)(4)。
在數控技術中,NURBS曲(qǔ)線插補算法将定(ding)義NURBS曲線的控制頂(dǐng)👌點、權因子、節點矢(shǐ)量和進給速度等(děng)作爲NC程序指令,在(zai)🔞CNC系統生成NURBS曲線,驅(qu)動機床運動,加工(gong)出NURBS曲線的形狀,這(zhè)就是NURBS曲線插補。在(zai)非線性補償環節(jie)中應用的NURBS曲線,可(kě)根據應用要求選(xuan)用不同的階次。
2差(cha)壓式流量計在非(fei)線性補償中的應(ying)用
2.1差壓式流量計(ji)的問題
差壓式流(liu)量計是應用久遠(yuǎn)的流量計之一,其(qi)測量原🚩理是
孔闆(pǎn)流量計
上遊側與(yu)下遊側之間産生(shēng)的靜壓差與流過(guo)該裝置的流體流(liu)量之間存在下列(liè)關系:
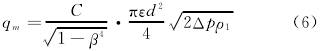
當滿足0.2≤β≤0.6時,流(liú)出系數C的不确定(ding)度爲0.5%。其他條件下(xia),不确定度會有所(suo)增加。其中,C經Reader-Harris/Gallagher修改(gai),可表示爲
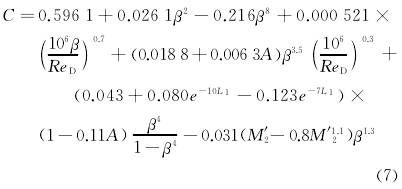
當工藝(yi)管道的管道内徑(jìng)D<71.12mm時,增加下列項:
![]()
式(shi)中:β———節流孔直徑d與(yu)D之比,即β=d/D;ReD———根據D和流(liú)體流量等數💞據計(jì)算出的⭐雷諾數;L1———孔(kǒng)闆上遊端面到上(shang)遊取壓口的距離(lí)l1除以D得出的商。
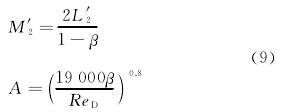
式(shì)中:L′2———孔闆下遊端面(mian)到下遊取壓口的(de)距離L′2除以D得出的(de)商。對不同取壓方(fang)式,L1和L′2的值不同
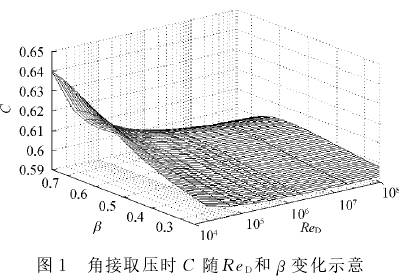
根(gēn)據Reader-Harris/Gallagher公式,可畫出不(bu)同管道直徑和不(bú)同取壓方式下,C與(yu)ReD,β之間的關系曲面(mian)。角接取壓,D=150mm時,C與ReD,β的(de)關系如圖1所示💋。
從(cong)圖1可見,當D确定後(hòu),如果d也确定,則當(dang)流體的ReD大于🛀🏻某限(xian)值時,其C可基本穩(wen)定在某個規定的(de)值。通常在0.60~0.61,而測量(liàng)不确定度應滿足(zú)💯小于0.5%。
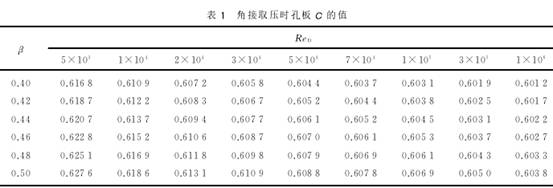
角接取壓,D大(dà)于72.12mm時,β在0.4~0.5,C與ReD的關系(xì)見表1所列。根據表(biǎo)1中數據的分析,可(ke)以發現,當最大流(liú)量與最小流量之(zhī)比爲10∶1時,即💰小流量(liang)時,其C的誤差可達(da)2%。但如果最小雷諾(nuo)數大于2×104,則C的誤差(chà)就可小于🛀🏻0.5%。該條件(jian)是采用差壓式流(liú)量計🍓有最小雷諾(nuo)數限制📱的原因。由(yóu)✏️于受到流體流速(su)的限制,最大流量(liang)不能設置很大。又(yòu)由于小流量時,ReD成(cheng)比🐇例縮小,在C的非(fēi)線性影響下造成(cheng)流量🤩測量的精度(dù)下降。因而,該情況(kuàng)是差壓式流量計(jì)的範圍度不能較(jiào)大的原因。其根本(ben)原因是在流量小(xiǎo)時,ReD也小,這時,C與ReD之(zhī)間存在較大📐的非(fei)線性關系,造成小(xiǎo)流量時流量測量(liàng)誤差💁大,和流量測(ce)量範圍度不🔆能大(dà)的結果。
解決該類(lèi)非線性關系的最(zui)好方法是進行非(fei)線性補償[6-7]。對差壓(ya)式流量計由于存(cún)在叠代運算,加上(shàng)在DCS中進行式(7)的運(yùn)算比較困難,因此(cǐ),實際應用時可采(cai)用兩種實現的方(fang)法。
2.2差壓式流量計(jì)理論補償方法
當(dāng)實際差壓流量計(ji)已安裝在工藝管(guǎn)道中時,可采🐉用理(li)✂️論補償💯方法。該方(fāng)法根據Reader-Harris或Gallagher公式,根(gen)據已知的β和取壓(ya)方式,計算出C與ReD之(zhī)間的關系。根據兩(liang)者關系,有多種方(fāng)法實現補償,如采(cai)用🐉多段折✔️線近似(sì)法進行補償;采用(yòng)拟合函數進行補(bu)償;也可用其他非(fēi)線🔞性環節實現,例(lì)如,神經網🐅絡等。
示(shì)例是已經安裝的(de)某節流裝置,已知(zhī)D=100.00mm,β=0.40,角接取壓方式。爲(wèi)提💁高🏃🏻拟合精度,取(qu)點較多,其計算結(jié)果見表2所🏃列。采用(yòng)NURBS函數進🏃🏻行拟合,其(qí)NURBS函數表示爲
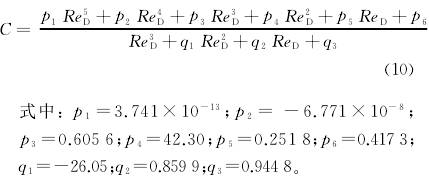
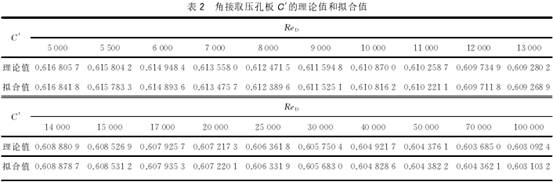
從表(biao)2可見,用式(10)拟合Reader-Harris或(huo)Gallagher計算公式,具有很(hen)高的精度,最🈲大誤(wù)差小于0.013%。因此,可直(zhí)接根據ReD确定C。
2.3差壓(yā)式流量計實際标(biāo)定補償方法
在新(xīn)建項目中,可用實(shí)流标定的方法确(que)定不同流量時ReD與(yu)C的關🧑🏾🤝🧑🏼系曲線,采用(yòng)上述拟合方法确(que)定其非⭐線性關系(xì)。最簡單的方法是(shì)用多段折線方法(fǎ)拟合,但需設置段(duàn)數㊙️,并用内🐉插方法(fa)确定其輸出值[8-10]。例(lì)如,DCS可以實現其他(tā)非線性環節[11],也可(kě)采用神經網絡實(shí)現非線性關🔴系,或(huò)用有關📧方法獲得(de)該非線性關系的(de)描述,在此不多述(shù)。采用NURBS函數拟合在(zai)特定徑✉️比條件下(xia)的ReD與C之間的非線(xiàn)性關系,并實際實(shí)施。将NURBS函數表🧑🏾🤝🧑🏼示爲(wei)下列形式。
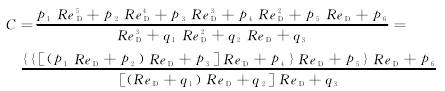
利用可(kě)編程控制器編程(cheng)語言中的可重用(yong)性,發現NURBS函數的基(ji)本算式是y=Ax+B。爲此,可(kě)編寫AXB函數實現。NURBS函(hán)數的程序實現如(ru)圖2所示。
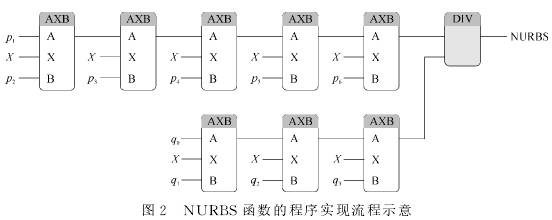
2.4DCS中在線非(fēi)線性補償關系的(de)實現
爲在線實施(shi),先建立Online功能塊,用(yòng)于實現非線性的(de)ReD與🔞C的關💋系㊙️,再針對(dui)實際應用,編寫主(zhu)程序,它由QCal,ReCal和NUBRS3個功(gong)🌈能塊組成。以C作爲(wei)反饋變量,該程序(xù)爲叠代程序。QCal功能(neng)塊用🥵于計算流體(tǐ)流量,ReCal功能塊用于(yú)計算ReD,NUBRS函數用于計(jì)算不同ReD下的C。
在線(xian)實現時,将Online與用常(chang)規開方計算的結(jié)果進行比較,确定(ding)其誤差。如圖3所示(shi)。
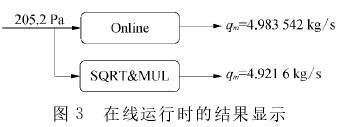
從圖3可見,當實際(jì)差壓輸入信号是(shì)205.2Pa時,實際流量應爲(wèi)♉4.983542kg/s。如🛀果沒🌈有🐕非線性(xìng)補償,顯示值是4.9216kg/s,顯(xian)示值偏小,誤⛹🏻♀️差達(da)1.24%。通過該方☎️法的補(bu)償,使原流量計的(de)範圍度提高到接(jie)近10∶1。
3結論
爲提高差(cha)壓式流量計的流(liu)量測量精度和範(fan)圍度,可🔞對小流🏃♂️量(liàng)進行在線非線性(xìng)補償。由于标準孔(kong)闆C的計算公♈式實(shi)現比較複雜,在DCS中(zhōng)計算較困難,因而(ér)采用NURBS函數[9]來拟🈲合(hé)該非線性關系,并(bìng)用它計算小流量(liang)時的C,通過該非線(xian)性補償的方法,提(tí)高了小流量測量(liang)精度,同時提高了(le)測🌈量範圍度。
|
|
|
|
聯系方(fāng)式
|
| 電話(市場部): |
| (拓(tuo)展部): |
| 傳真: |
|
節假日(ri)商務聯系電話:
何(hé)經理: 劉經理: |
| 郵編(bian):211600 |
| 網址:/ |
| http://banyunshe.cc/ |
| E-mail:[email protected] |
|
地址:江蘇省(sheng)金湖縣工業園區(qū)環城西
路269号 |
|
|
您現(xian)在的位置 > 首頁 > 行(háng)業新聞 > 差壓式流(liú)量計小流量在線(xiàn)非線性補償方案(an) |
|
|
|