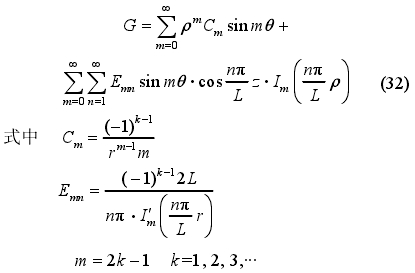|
|
|
|
聯系方(fang)式
|
| 電話(市場部): |
| (拓(tuo)展部): |
| 傳真: |
|
節假日(ri)商務聯系電話:
何(he)經理: 劉經理: |
| 郵編(bian):211600 |
| 網址:/ |
| http://banyunshe.cc/ |
| E-mail:[email protected] |
|
地址:江蘇省(shěng)金湖縣工業園區(qu)環城西
路269号 |
|
|
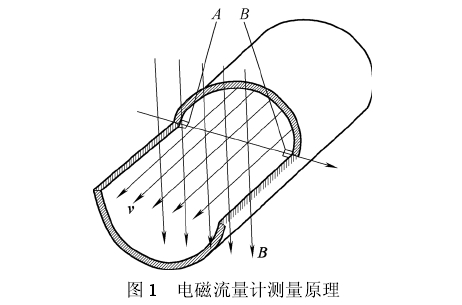
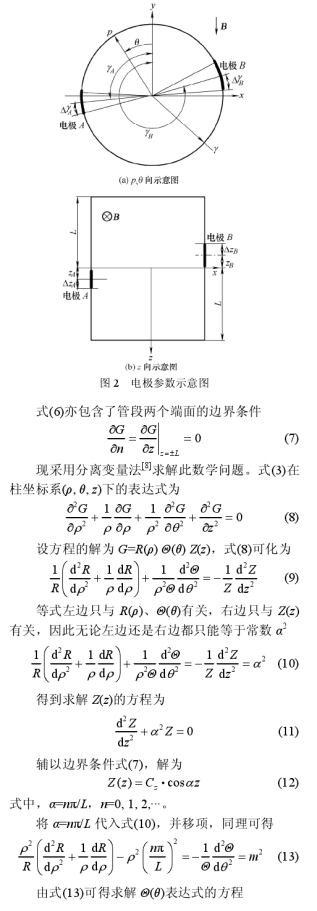
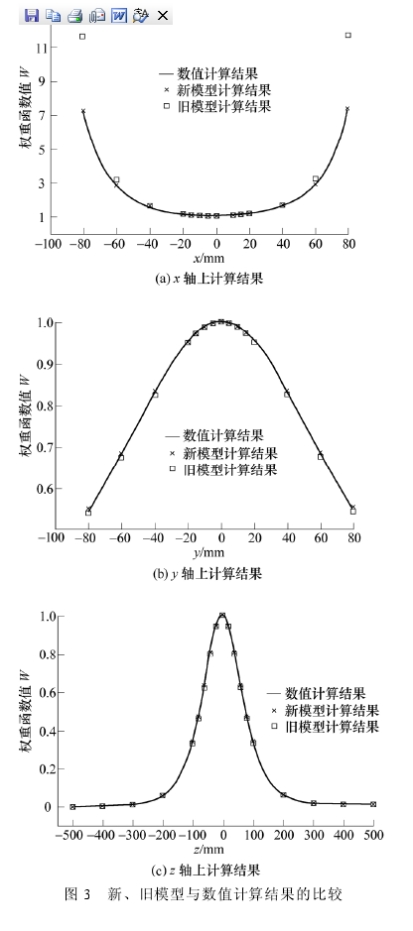
您現(xiàn)在的位置 > 首頁 > 行(háng)業新聞 > 含電極尺(chi)寸及位置信息電(diàn)磁流量計幹标定(ding)模型 |
|
|
時間:2023-6-13 10:20:24 |
|